Overview
I study machine learning, particularly non‑parametric statistics, where I develop algorithms with theoretical guarantees and explore the underlying mathematics of non‑parametric problems. On the deep‑learning side I focus on deep anomaly detection and, more recently, deep probabilistic models.
Potential collaborators & students: I don’t control hiring budgets, but I’m happy to co‑advise students or discuss collaborations.
Structured Non‑Parametric Statistics
Classical non‑parametric estimators suffer from the curse of dimensionality. Real‑world data, however, has structure—for instance, nearby pixels in images are highly correlated while distant pixels are nearly independent. By encoding such structure (e.g. with graphical models) we can obtain non‑parametric methods that scale to high‑dimensional settings.
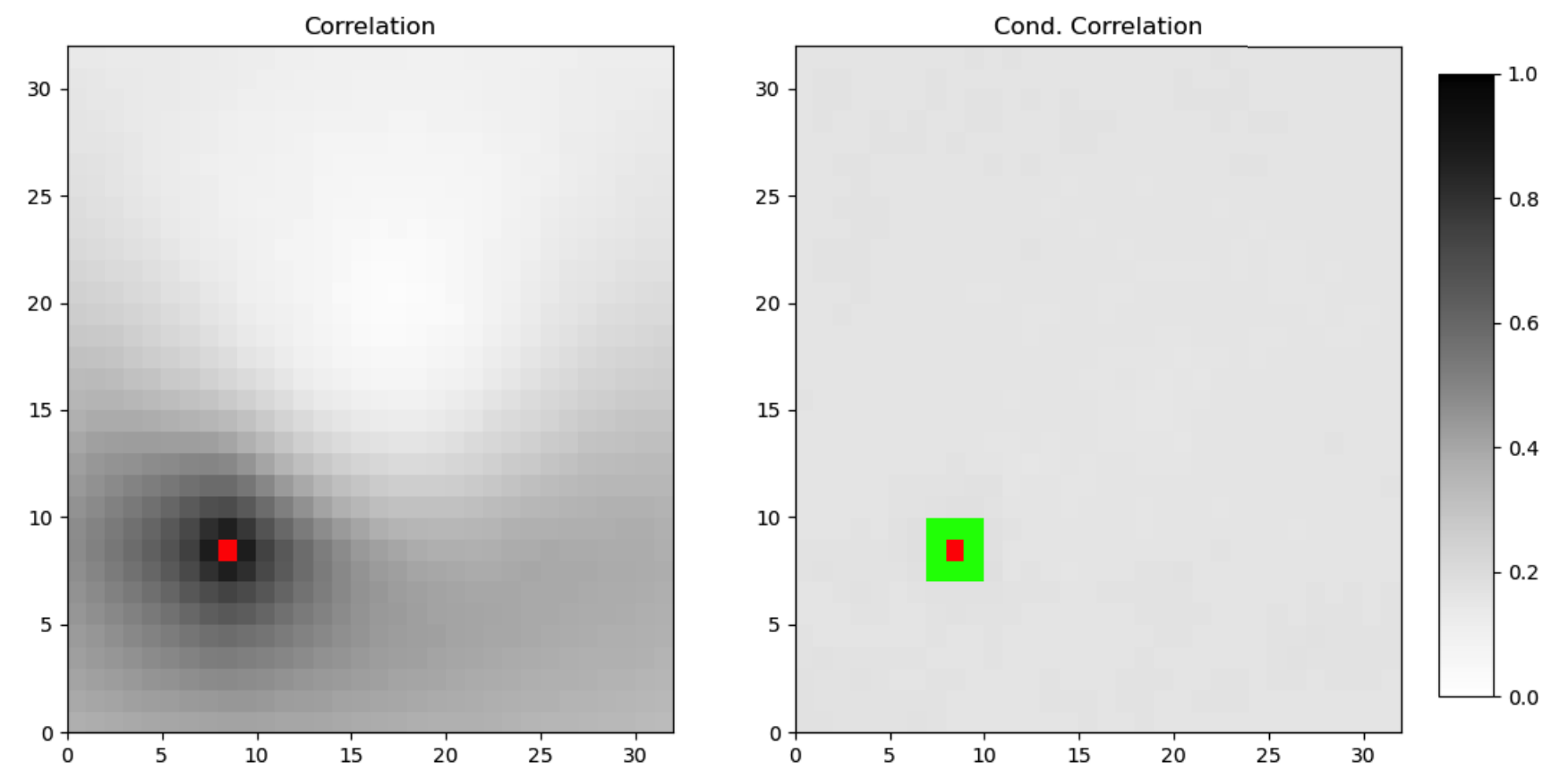
Conditioning introduces independence in images → Markov random fields capture this structure.
Low‑Rank Non‑Parametrics
Low‑rank ideas power matrix completion and compressed sensing; I extend them to the infinite‑dimensional realm of non‑parametric density estimation. Existing finite‑dimensional techniques don’t transfer directly, so new algorithms and analyses are required.
- Improving Non‑Parametric Density Estimation with Tensor Decompositions, arXiv 2020
- Beyond Smoothness: Incorporating Low‑Rank Analysis into Non‑Parametric Density Estimation, NeurIPS 2021
Non‑Parametric Mixture Modelling
Mixture models capture heterogeneity by representing data as a convex combination of component distributions. I study the setting with no parametric assumptions on the components, but where groups of samples are known to come from the same component—linking the problem to non‑negative tensor factorisation.
- An Operator Theoretic Approach to Non‑Parametric Mixture Models, Annals of Statistics 2019
- Consistent Estimation of Identifiable Non‑Parametric Mixture Models from Grouped Observations, NeurIPS 2020
- Generalised Identifiability Bounds for Mixture Models with Grouped Samples, IEEE T‑IT 2024
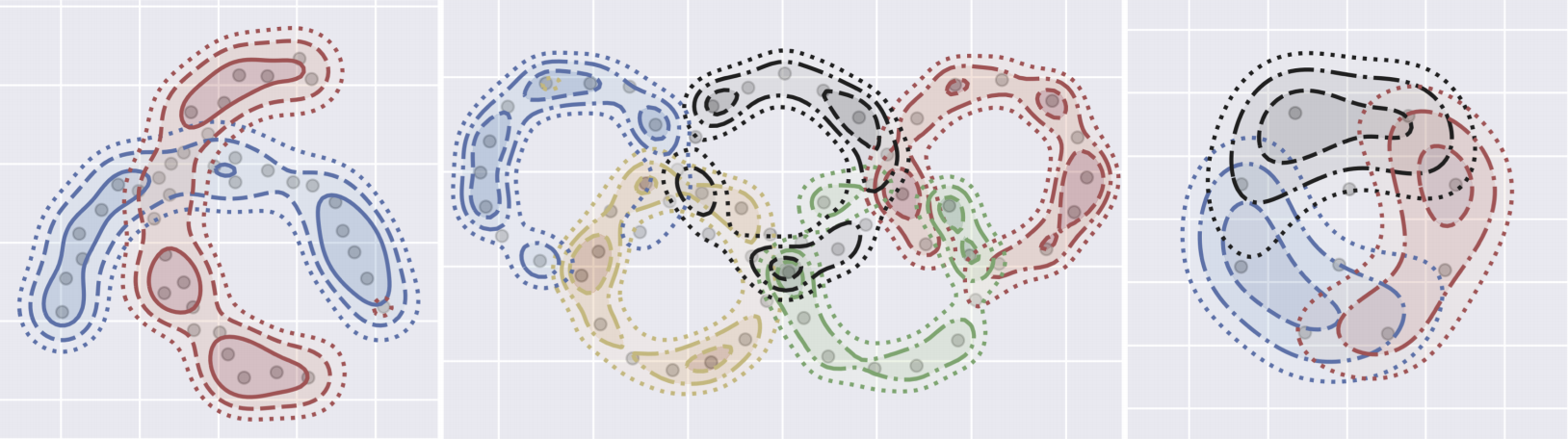
Our theory enables provably correct clustering even with overlapping components.
Deep Anomaly Detection
Anomaly detection flags unusual samples relative to nominal data. In high‑dimensional domains (images, medical scans, industrial QC) deep one‑class methods such as Deep SVDD excel.
- Deep One‑Class Classification, ICML 2018 [code]
- Image Anomaly Detection with GANs, ECML PKDD 2018
- Deep Semi‑Supervised Anomaly Detection, ICLR 2020 [code]
- Explainable Deep One‑Class Classification, ICLR 2021 [code]
- Transfer‑Based Semantic Anomaly Detection, ICML 2021 [code]
- A Unifying Review of Deep and Shallow Anomaly Detection, Proceedings of the IEEE 2021

CIFAR‑10: normal examples (left) vs. anomalies (right).
Other Topics
- Supervised Density Estimation: incorporating low‑likelihood samples directly into density estimators. A Proposal for Supervised Density Estimation, NeurIPS Prereg Workshop 2020
- Robust Kernel Density Estimation:
- Robust KDE by Scaling & Projection in Hilbert Space, NeurIPS 2014
- Consistency of Robust Kernel Density Estimators, COLT 2013